¿Qué son las magnitudes escalares y vectoriales?

La física es una ciencia que intenta describir el comportamiento del universo a través de unos conceptos y principios que tienen una base matemática. Así, las magnitudes físicas son los valores matemáticos asociados a las propiedades medibles de un objeto o sistema físico.

Muchas de estas propiedades se pueden describir completamente mediante un número o valor numérico, mientras que otras necesitan conocer la orientación en el espacio en la que se producen.

Por ejemplo, imagina que nos vendamos los ojos y alguien nos guía hasta un objeto diciendo: 3 metros, 2 metros, 8 metros. No llegaríamos nunca o lo haríamos por pura casualidad.

En cambio, si nos dice 3 metros hacia adelante, 2 a la derecha y 8 a la izquierda, llegaríamos al objetivo sin ningún problema.

Para describir el movimiento de un objeto en un sistema físico no basta con conocer cuanto se ha desplazado el objeto, sino también hacia donde, es decir, es necesario conocer la dirección y sentido de desplazamiento. Lo mismo ocurre si conocemos solo el valor numérico de la velocidad a la que se desplaza un objeto; nos faltaría conocer la dirección y sentido del desplazamiento para poder describir su movimiento.

Magnitudes escalares y vectoriales

Las magnitudes que describen propiedades no asociadas con una orientación se conocen como magnitudes escalares; matemáticamente se representan mediante un valor numérico seguido del símbolo de la unidad en la que se esté midiendo la propiedad.

Las magnitudes asociadas a una orientación (dirección y sentido) se conocen como magnitudes vectoriales; matemáticamente se representan mediante vectores y se suelen expresar con una flechita sobre el símbolo (por ejemplo ).

1. Magnitudes escalares: magnitud física que queda descrita completamente mediante un valor numérico. Ejemplos de magnitudes escalares son masa, volumen, temperatura, densidad, presión, energía, carga eléctrica, etc.
2. Magnitudes vectoriales: magnitud física que es descrita mediante un valor numérico o magnitud, llamada módulo, y una orientación en el espacio. La orientación se describe mediante un sistema de coordenadas cartesianas (x, y, z). Por ejemplo, son magnitudes vectoriales la aceleración, la velocidad de desplazamiento, campo eléctrico, el peso o cualquier otra forma de fuerza, por ejemplo la fuerza de la gravedad.

Muchas magnitudes vectoriales se suelen utilizar coloquialmente sin atender a su carácter vectorial. lo que suele causar mucha confusión. Por ejemplo, es habitual hablar de la velocidad de un objeto sin atender al sentido de desplazamiento, pero en física eso sería la celeridad o rapidez, no la velocidad, pues la velocidad en física se trata como una magnitud vectorial.

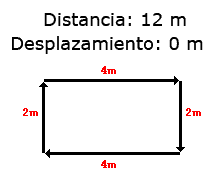
La comparación de las magnitudes vectoriales requiere la comparación de su vector y no solo de su valor, por lo que es más compleja que la comparación de magnitudes escalares. Vamos a suponer que caminamos 4 metros al este, 2 metros al sur, 4 metros al oeste y 2 metros al norte:

La distancia recorrida habrá sido de 12 metros, pero el desplazamiento hará sido 0 metros, pues la localización final e inicial es la misma. Esto se debe a que la suma de dos vectores de igual magnitud pero sentido opuesto es igual a cero, los dos vectores se anulan. Así pues, la suma de los cuatro vectores que describen el movimiento realizado en el ejemplo anterior sería cero, no así la distancia recorrida.

Es fácil de entender si imaginamos dos fuerzas opuestas de igual intensidad. Las dos fuerzas son positivas pero se anulan mutuamente. Por ejemplo, si una persona empuja un objeto dese atrás y otra persona lo empuja desde delante con la misma fuerza, las dos fuerzas se anularían y el objeto no se movería. La fuerza neta aplicada sobre el objeto sería cero.

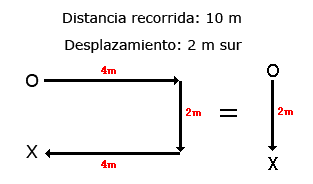
Si ahora nos moviésemos 4 m al este, 2 al sur y 4 al oeste, la distancia recorrida habría sido de 10 m y el desplazamiento de 2 m al sur, pues los 4 m al este y lo 4 al oeste se anularían:

La comparación de magnitudes se puede complicar aún más. Por ejemplo, el desplazamiento no puede ser solo hacia el norte, al sur o al oeste, también puede ser hacia arriba o hacia abajo. Es decir, los vectores pueden tener una dirección y un sentido tridimensional.

Diferencias clave entre magnitud escalar y vectorial

1. Una magnitud escalar se puede describir como aquella que solo tiene una característica: el valor numérico. Una magnitud vectorial tiene dos características: valor numérico y valor vectorial (orientación en el espacio).
2. Las magnitudes escalares solo cambian cuando cambia su valor o magnitud. Las magnitudes vectoriales cambian cuando cambia su magnitud, su orientación o ambas.
3. Las operaciones con magnitudes escalares siguen las reglas comunes del álgebra como la suma, la resta o la multiplicación. Las operaciones con magnitudes vectoriales siguen el álgebra líneal.
4. Al comparar dos magnitudes escalares, basta con considerar el valor numérico. Al comparar una magnitud vectorial es necesario considerar también su orientación en el espacio.
5. Una magnitud escalar se puede dividir entre otra magnitud escalar, pero dos magnitudes vectoriales no se pueden dividir entre sí, ya que están definidas por vectores y la división entre vectores no es posible.